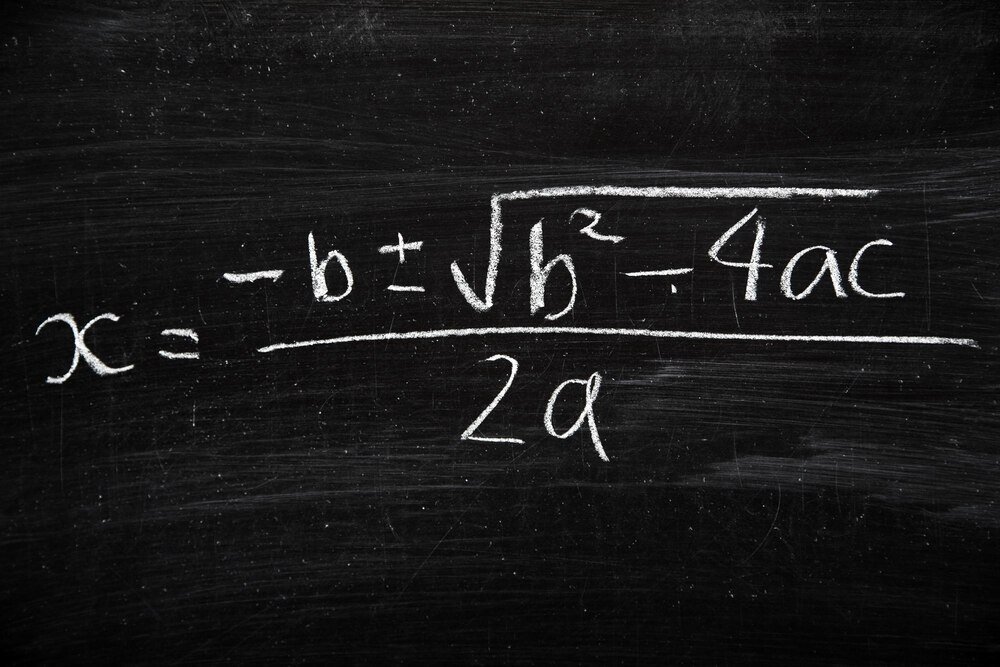Postać iloczynowa funkcji kwadratowej
Funkcja kwadratowa to jeden z podstawowych typów funkcji, z którym spotykamy się w matematyce. Zrozumienie jej różnych postaci, szczególnie postaci iloczynowej, otwiera przed nami wiele możliwości rozwiązywania problemów matematycznych. W tym artykule poznasz, czym jest postać iloczynowa funkcji kwadratowej, jak obliczyć miejsca zerowe oraz deltę, a także jak wykorzystać tę wiedzę w praktyce.
Podstawowe informacje o funkcji kwadratowej
Funkcja kwadratowa to funkcja opisana wzorem f(x) = ax² + bx + c, gdzie a, b, c są liczbami rzeczywistymi, a współczynnik a jest różny od zera. Jest to tak zwana postać ogólna (standardowa) funkcji kwadratowej. Wykresem funkcji kwadratowej jest parabola, która może być skierowana ramionami do góry (gdy a > 0) lub do dołu (gdy a < 0). Oprócz postaci ogólnej, funkcję kwadratową możemy zapisać również w postaci kanonicznej: f(x) = a(x - p)² + q, gdzie punkt (p, q) jest wierzchołkiem paraboli. Postać iloczynowa funkcji kwadratowej ma wzór: f(x) = a(x – x₁)(x – x₂), gdzie x₁ i x₂ to miejsca zerowe funkcji, czyli wartości argumentu x, dla których funkcja przyjmuje wartość 0. Innymi słowy, są to punkty, w których wykres funkcji przecina oś OX.
Delta funkcji kwadratowej
Aby znaleźć miejsca zerowe funkcji kwadratowej, musimy najpierw obliczyć deltę (Δ). Delta to wyrażenie, które pozwala określić liczbę miejsc zerowych funkcji kwadratowej.
Wzór na deltę dla funkcji kwadratowej f(x) = ax² + bx + c wynosi:
Δ = b² – 4ac
Wartość delty informuje nas o liczbie miejsc zerowych funkcji:
- Jeśli Δ > 0, funkcja ma dwa różne miejsca zerowe (x₁ ≠ x₂)
- Jeśli Δ = 0, funkcja ma jedno miejsce zerowe (x₁ = x₂)
- Jeśli Δ < 0, funkcja nie ma miejsc zerowych w zbiorze liczb rzeczywistych
Ciekawostka: Delta została wprowadzona do matematyki przez indyjskiego matematyka Bhāskarę II w XII wieku, choć sama metoda rozwiązywania równań kwadratowych była znana już w starożytnym Babilonie.
Wyznaczanie miejsc zerowych (x₁ i x₂)
Gdy znamy już wartość delty, możemy przystąpić do obliczania miejsc zerowych funkcji kwadratowej. W zależności od wartości delty, stosujemy odpowiednie wzory:
Jeśli Δ > 0, mamy dwa różne miejsca zerowe:
x₁ = (-b – √Δ) / (2a)
x₂ = (-b + √Δ) / (2a)
Jeśli Δ = 0, mamy jedno miejsce zerowe (tzw. miejsce podwójne):
x₀ = x₁ = x₂ = -b / (2a)
Jeśli Δ < 0, funkcja nie ma miejsc zerowych w zbiorze liczb rzeczywistych.
Interpretacja geometryczna miejsc zerowych
Z geometrycznego punktu widzenia, miejsca zerowe to punkty, w których wykres funkcji (parabola) przecina oś OX. Jeśli delta jest dodatnia, parabola przecina oś OX w dwóch różnych punktach. Gdy delta jest równa zero, parabola dotyka osi OX w jednym punkcie (jest to wierzchołek paraboli, jeśli leży on na osi OX). Natomiast gdy delta jest ujemna, parabola nie przecina osi OX i znajduje się całkowicie powyżej lub poniżej tej osi.
Przejście z postaci ogólnej do iloczynowej
Aby przekształcić funkcję z postaci ogólnej f(x) = ax² + bx + c do postaci iloczynowej f(x) = a(x – x₁)(x – x₂), należy wykonać następujące kroki:
1. Oblicz deltę: Δ = b² – 4ac
2. Sprawdź wartość delty:
– Jeśli Δ < 0, postać iloczynowa nie istnieje w zbiorze liczb rzeczywistych
- Jeśli Δ ≥ 0, przejdź do kolejnego kroku
3. Oblicz miejsca zerowe x₁ i x₂
4. Zapisz funkcję w postaci iloczynowej: f(x) = a(x - x₁)(x - x₂)
Przykład rozwiązania
Przekształćmy funkcję f(x) = 2x² – 8x + 6 do postaci iloczynowej.
Krok 1: Obliczamy deltę.
Δ = b² – 4ac = (-8)² – 4 · 2 · 6 = 64 – 48 = 16
Krok 2: Ponieważ Δ > 0, funkcja ma dwa miejsca zerowe.
Krok 3: Obliczamy miejsca zerowe.
x₁ = (-b – √Δ) / (2a) = (8 – 4) / 4 = 1
x₂ = (-b + √Δ) / (2a) = (8 + 4) / 4 = 3
Krok 4: Zapisujemy funkcję w postaci iloczynowej.
f(x) = 2(x – 1)(x – 3)
Możemy sprawdzić poprawność naszego rozwiązania, rozwijając nawias:
f(x) = 2(x – 1)(x – 3) = 2(x² – 3x – x + 3) = 2(x² – 4x + 3) = 2x² – 8x + 6
Jak widać, otrzymaliśmy wyjściową funkcję, co potwierdza poprawność naszych obliczeń.
Zastosowania postaci iloczynowej
Postać iloczynowa funkcji kwadratowej ma wiele praktycznych zastosowań, które znacząco upraszczają rozwiązywanie problemów matematycznych:
1. Łatwe odczytanie miejsc zerowych – są one bezpośrednio widoczne w zapisie funkcji, co eliminuje potrzebę rozwiązywania równania kwadratowego.
2. Szybkie wyznaczanie wartości funkcji – szczególnie przydatne, gdy x jest bliski miejscom zerowym. Wystarczy podstawić wartość x i wykonać proste mnożenie.
3. Rozwiązywanie nierówności kwadratowych – korzystając z postaci iloczynowej, możemy łatwo określić, dla jakich wartości x funkcja przyjmuje wartości dodatnie lub ujemne, analizując znaki poszczególnych czynników.
4. Analiza funkcji – postać iloczynowa ułatwia badanie własności funkcji, takich jak monotoniczność czy ekstrema, ponieważ jasno pokazuje, jak zachowuje się funkcja w okolicy miejsc zerowych.
5. Zastosowania w fizyce i innych naukach – np. przy analizie ruchu ciał, obwodów elektrycznych czy problemów optymalizacyjnych, gdzie często potrzebujemy znać punkty, w których funkcja przyjmuje wartość zero.
Pamiętaj: Postać iloczynowa istnieje tylko wtedy, gdy funkcja kwadratowa ma miejsca zerowe w zbiorze liczb rzeczywistych, czyli gdy delta jest nieujemna (Δ ≥ 0).
Opanowanie umiejętności przekształcania funkcji kwadratowej do postaci iloczynowej oraz obliczania delty i miejsc zerowych jest niezwykle przydatne w matematyce. Te umiejętności stanowią fundament do rozwiązywania bardziej zaawansowanych problemów matematycznych, a także znajdują zastosowanie w wielu dziedzinach nauki i techniki.
Pamiętaj, że regularne ćwiczenie rozwiązywania różnych typów zadań z funkcjami kwadratowymi jest kluczem do opanowania tego tematu. Warto również zwracać uwagę na interpretację geometryczną, która często pomaga w lepszym zrozumieniu algebraicznych przekształceń i daje pełniejszy obraz analizowanego problemu.