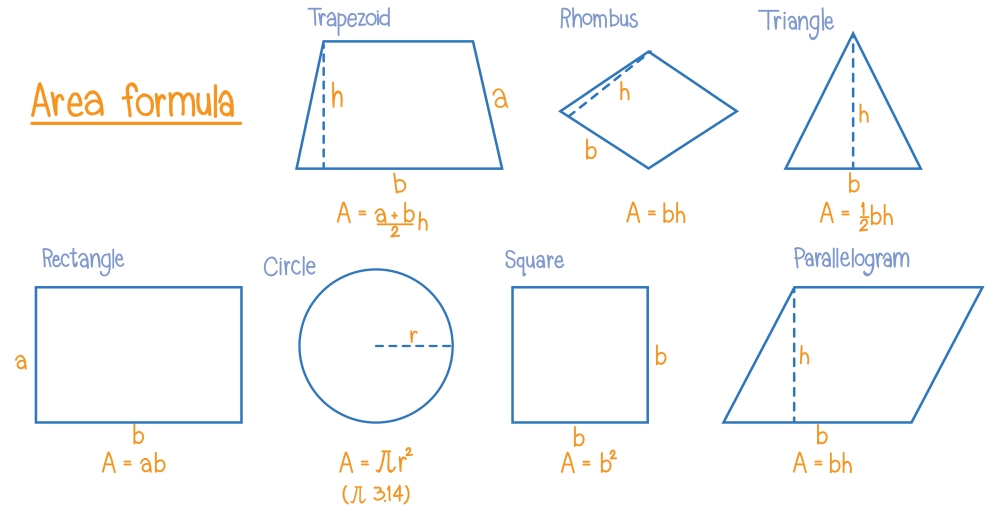
Pole trapezu to jeden z podstawowych wzorów geometrycznych, który znajduje zastosowanie zarówno w matematyce szkolnej, jak i w praktycznych zagadnieniach technicznych. Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych – te boki nazywamy podstawami trapezu.
Czym jest trapez?
Trapez to czworokąt, który posiada co najmniej jedną parę równoległych boków. Te równoległe boki nazywamy podstawami trapezu (oznaczamy je jako \(a\) i \(b\)), a odległość między nimi to wysokość trapezu (oznaczana jako \(h\)).
Rodzaje trapezów:
- Trapez równoramienny – ramiona (boki nierównoległe) są równej długości
- Trapez prostokątny – jedno z ramion jest prostopadłe do podstaw
- Trapez różnoboczny – ramiona mają różne długości
Wzór na pole trapezu
Pole trapezu obliczamy według wzoru:
$$P = \frac{(a + b) \cdot h}{2}$$
Gdzie:
- \(P\) – pole trapezu
- \(a\) – długość pierwszej podstawy (dolnej)
- \(b\) – długość drugiej podstawy (górnej)
- \(h\) – wysokość trapezu (odległość między podstawami)
Alternatywny zapis wzoru:
$$P = \frac{a + b}{2} \cdot h$$
Możemy to odczytać jako: pole trapezu jest równe średniej arytmetycznej długości podstaw pomnożonej przez wysokość.
Wizualizacja trapezu
Poniższy interaktywny wykres pokazuje trapez wraz z oznaczeniem jego podstaw i wysokości:
Wzór można wyprowadzić geometrycznie – trapez można podzielić na prostokąt i dwa trójkąty, lub potraktować jako średnią z dwóch prostokątów o wysokości \(h\) i podstawach \(a\) oraz \(b\).
Przykłady obliczania pola trapezu
Przykład 1: Podstawowy trapez
Oblicz pole trapezu o podstawach \(a = 8\) cm, \(b = 5\) cm i wysokości \(h = 4\) cm.
Rozwiązanie:
Podstawiamy dane do wzoru:
$$P = \frac{(a + b) \cdot h}{2} = \frac{(8 + 5) \cdot 4}{2} = \frac{13 \cdot 4}{2} = \frac{52}{2} = 26 \text{ cm}^2$$
Odpowiedź: Pole trapezu wynosi 26 cm²
Przykład 2: Trapez z większymi liczbami
Działka ma kształt trapezu o podstawach 25 m i 18 m oraz wysokości 12 m. Oblicz jej pole.
Rozwiązanie:
$$P = \frac{(25 + 18) \cdot 12}{2} = \frac{43 \cdot 12}{2} = \frac{516}{2} = 258 \text{ m}^2$$
Odpowiedź: Pole działki wynosi 258 m²
Przykład 3: Obliczanie wysokości
Trapez ma pole 48 cm², podstawy wynoszą 7 cm i 9 cm. Oblicz wysokość trapezu.
Rozwiązanie:
Przekształcamy wzór na pole, aby wyznaczyć wysokość:
$$P = \frac{(a + b) \cdot h}{2}$$
$$h = \frac{2P}{a + b} = \frac{2 \cdot 48}{7 + 9} = \frac{96}{16} = 6 \text{ cm}$$
Odpowiedź: Wysokość trapezu wynosi 6 cm
Przykład 4: Obliczanie podstawy
Trapez ma pole 60 cm², jedną podstawę \(a = 10\) cm i wysokość \(h = 8\) cm. Oblicz długość drugiej podstawy.
Rozwiązanie:
Przekształcamy wzór:
$$P = \frac{(a + b) \cdot h}{2}$$
$$a + b = \frac{2P}{h}$$
$$b = \frac{2P}{h} – a = \frac{2 \cdot 60}{8} – 10 = \frac{120}{8} – 10 = 15 – 10 = 5 \text{ cm}$$
Odpowiedź: Druga podstawa ma długość 5 cm
Interaktywny kalkulator pola trapezu
Skorzystaj z kalkulatora, aby obliczyć pole trapezu lub wyznaczyć brakujące wymiary.
Kalkulator trapezu
Wzór na obwód trapezu
Obwód trapezu obliczamy sumując długości wszystkich jego boków:
$$Obw = a + b + c + d$$
Gdzie \(a\) i \(b\) to podstawy, a \(c\) i \(d\) to ramiona trapezu.
Dla trapezu równoramiennego (gdzie \(c = d\)):
$$Obw = a + b + 2c$$
Trapez równoramienny – wzory dodatkowe
W trapezie równoramiennym ramiona mają równą długość. Jeśli znamy podstawy \(a\), \(b\) oraz wysokość \(h\), możemy obliczyć długość ramienia:
$$c = \sqrt{h^2 + \left(\frac{a-b}{2}\right)^2}$$
Ten wzór wynika z twierdzenia Pitagorasa zastosowanego do trójkąta prostokątnego utworzonego przez wysokość, ramię i część podstawy.
Zastosowania praktyczne pola trapezu
Wzór na pole trapezu znajduje liczne zastosowania w życiu codziennym i nauce:
- Geodezja i miernictwo: Obliczanie powierzchni działek o nieregularnych kształtach
- Budownictwo: Projektowanie dachów, schodów, pochylni
- Architektura: Projektowanie sal widowiskowych, amfiteatrów
- Inżynieria: Przekroje kanałów, rowów melioracyjnych
- Rolnictwo: Obliczanie powierzchni pól uprawnych
- Transport: Projektowanie skrzyżowań, rond
Metoda wyprowadzenia wzoru
Wzór na pole trapezu można wyprowadzić na kilka sposobów:
Metoda 1: Podział na prostokąt i trójkąty
Trapez można podzielić na prostokąt o wymiarach \(b \times h\) oraz dwa trójkąty. Suma ich pól daje:
$$P = b \cdot h + \frac{(a-b) \cdot h}{2} = b \cdot h + \frac{a \cdot h}{2} – \frac{b \cdot h}{2} = \frac{2bh + ah – bh}{2} = \frac{(a+b) \cdot h}{2}$$
Metoda 2: Średnia z prostokątów
Wyobraźmy sobie dwa prostokąty: jeden o podstawie \(a\) i wysokości \(h\), drugi o podstawie \(b\) i wysokości \(h\). Trapez ma pole równe średniej arytmetycznej tych prostokątów:
$$P = \frac{a \cdot h + b \cdot h}{2} = \frac{(a+b) \cdot h}{2}$$
Porównanie figur geometrycznych
| Figura | Wzór na pole | Warunek |
|---|---|---|
| Prostokąt | \(P = a \cdot b\) | Trapez, gdzie \(a = b\) |
| Równoległobok | \(P = a \cdot h\) | Trapez, gdzie podstawy są równe |
| Trapez | \(P = \frac{(a+b) \cdot h}{2}\) | Dwie równoległe podstawy |
| Trójkąt | \(P = \frac{a \cdot h}{2}\) | Trapez, gdzie \(b = 0\) |
Zadania do samodzielnego rozwiązania
Zadanie 1: Oblicz pole trapezu o podstawach 12 cm i 8 cm oraz wysokości 5 cm.
Zadanie 2: Trapez ma pole 84 m², podstawy wynoszą 10 m i 18 m. Oblicz wysokość.
Zadanie 3: Działka ma kształt trapezu równoramiennego o podstawach 30 m i 20 m oraz wysokości 15 m. Oblicz pole działki.
Zadanie 4: Trapez ma pole 60 cm², jedną podstawę 9 cm i wysokość 8 cm. Oblicz długość drugiej podstawy.
Zadanie 5: Oblicz pole trapezu prostokątnego, którego podstawy wynoszą 14 cm i 10 cm, a dłuższe ramię ma długość 5 cm.
Zadanie 6: Trapez równoramienny ma podstawy 16 cm i 10 cm oraz ramiona długości 5 cm. Oblicz jego pole.
📝 Kliknij, aby zobaczyć odpowiedzi
Odpowiedź 1: P = (12+8)·5/2 = 20·5/2 = 50 cm²
Odpowiedź 2: h = 2·84/(10+18) = 168/28 = 6 m
Odpowiedź 3: P = (30+20)·15/2 = 50·15/2 = 375 m²
Odpowiedź 4: b = 2·60/8 – 9 = 15 – 9 = 6 cm
Odpowiedź 5: Wysokość h = 5 cm (ramię jest wysokością), P = (14+10)·5/2 = 60 cm²
Odpowiedź 6: Najpierw wysokość: h = √(5² – 3²) = √16 = 4 cm, potem pole: P = (16+10)·4/2 = 52 cm²
Najczęstsze błędy przy obliczaniu pola trapezu
- Pomylenie wzorów: Stosowanie wzoru na pole prostokąta \(P = a \cdot h\) zamiast wzoru na pole trapezu
- Zapomnienie o dzieleniu przez 2: Obliczanie \((a+b) \cdot h\) bez dzielenia wyniku przez 2
- Mylenie podstaw z ramionami: Podstawy to boki równoległe, nie wszystkie boki trapezu
- Błędne jednostki: Jeśli podstawy są w metrach, a wysokość w centymetrach, trzeba najpierw przeliczyć na te same jednostki
- Mylenie wysokości z ramieniem: Wysokość to odległość między podstawami mierzona prostopadle, nie długość ramienia
Ciekawostki o trapezie
Środkowa trapezu: Odcinek łączący środki ramion trapezu nazywamy środkową. Jej długość wynosi:
$$m = \frac{a + b}{2}$$
A pole trapezu można obliczyć również jako:
$$P = m \cdot h$$
Przekątne trapezu równoramiennego: W trapezie równoramiennym przekątne mają równą długość i można je obliczyć ze wzoru:
$$d = \sqrt{c^2 + a \cdot b}$$
gdzie \(c\) to długość ramienia.
Podsumowanie
Pole trapezu to podstawowy wzór geometryczny, który należy zapamiętać:
$$P = \frac{(a + b) \cdot h}{2}$$
Kluczowe informacje:
- Trapez ma dwie równoległe podstawy (\(a\) i \(b\))
- Wysokość (\(h\)) to odległość między podstawami mierzona prostopadle
- Wzór można odczytać jako: średnia z podstaw razy wysokość
- Przekształcając wzór, możemy obliczyć wysokość lub drugą podstawę
- Trapez to uogólnienie innych figur (prostokąta, równoległoboku, trójkąta)
Praktyczne zastosowania trapezu sprawiają, że ten wzór jest często wykorzystywany w geodezji, budownictwie i inżynierii.